该书对于命题逻辑、谓词逻辑、通过模型检测进行验证及程序验证有较详细的讲解。
命题逻辑
命题逻辑是一种基于命题(propositions)的逻辑语言,用来对计算机科学领域中所遇到的情境进行建模,并可以进行形式化推理。命题逻辑本质上是符号的(symbolic),将自然语言符号化得以重点关注论证的机理。因为计算机系统或软件的规范就是这些判断句的序列。进而,它展示了对规范自动化处理的可能性。
自然演绎及推断规则
在命题逻辑中形式化推理的规则称为自然演绎,其中有一组证明规则。规则允许我们由其他公式推断出新的公式。通过逐次应用这些规则,我们可以由一组前提推断出一个结论。这种意图记为:
$\phi_1, \phi_2, \cdots, \phi_n \vdash \psi$
该表达式称为矢列。如果可以找到它的证明则该矢列是有效的。
在这个过程中使用的证明规则如下表:
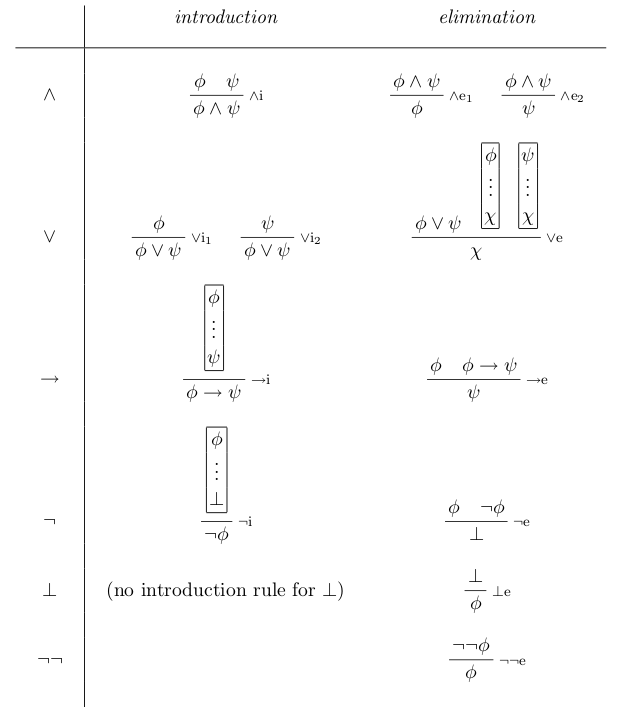
语法及语义
使用这些规则就可以从一个公式推断出另一个公式。当我们应用这些规则构造证明的时候,实际上只需要关注矢列的语法结构。从语法上来讲,我们使用的公式必须是合式的,由BNF表示如下:
$\phi ::= p ~|~ (\neg \phi)~|~ (\phi \wedge \phi) ~|~(\phi \vee \phi) ~|~(\phi \rightarrow \phi)$
语法上的公式表达了从前提到结论的一种有效的推理演算,是前提和结论之间关系的一种描述。从语义上讲还存在另一种描述:
$\phi_1, \phi_2, \cdots, \phi_n \models \psi$
这种描述基于前提和结论中的原子公式的“真值”,以及逻辑连接词如何影响这些真值。
从语法和语义两个角度来看命题逻辑:就公式$\phi\rightarrow\psi$和$\neg\phi\vee\psi$来看,从自然演绎的角度他们在句法上是完全不同的,但是使用真值表得到的语义信息是完全相同的。也就是说,他们两个公式是语义等价的。
命题逻辑的可靠性(soundness)
假设从前提$\phi_1, \phi_2, \cdots, \phi_n$出发可以得到$\psi$的证明则说$\phi_1, \phi_2, \cdots, \phi_n \vdash \psi$是有效的。若对使所有命题$\phi_1, \phi_2, \cdots, \phi_n$都赋值为T的一切赋值,$\psi$也赋值为T,则说$\phi_1, \phi_2, \cdots, \phi_n \models \psi$成立。
设$\phi_1, \phi_2, \cdots, \phi_n$和$\psi$是命题逻辑的公式。若$\phi_1, \phi_2, \cdots, \phi_n \vdash \psi$是有效的,则$\phi_1, \phi_2, \cdots, \phi_n \models \psi$成立。
可靠性的用处
语法上有效的表达在语义上一定是有效的。常常反过来用,语义上无效的表达在语法上也是站不住脚的。逻辑系统的可靠性可以用来确定有一些证明是不存在的。
例如:在命题逻辑系统中给定前提$\phi_1, \phi_2, \cdots, \phi_n$,能否证明$\psi$?这其实是在问:$\phi_1, \phi_2, \cdots, \phi_n \vdash \psi$是否是有效的。
如果这个前提和结论非常复杂,那么你很可能证明不出来,因为证明通常是需要一点灵感的,而灵感通常是难得的。但是,你证明不出来不能说明这个证明不存在。那我们应该怎么做呢?
有了可靠性定理,我们就可以将问题转化为:$\phi_1, \phi_2, \cdots, \phi_n \models \psi$是否是有效的。而这个问题,我们完全可以用真值表来确定。假如我们用真假表确定了, $\phi_1, \phi_2, \cdots, \phi_n \models \psi$是无效的, 那么,我们完全可以断言:$\phi_1, \phi_2, \cdots, \phi_n \vdash \psi$是无效的。即证明不存在。因为根据可靠性定理,如果$\phi_1, \phi_2, \cdots, \phi_n \vdash \psi$是有效的, 那么$\phi_1, \phi_2, \cdots, \phi_n \models \psi$是有效的,与我们根据真值表得出的结论相矛盾。
命题逻辑的完备性(completeness)
只要$\phi_1, \phi_2, \cdots, \phi_n \models \psi$成立,都存在矢列$\phi_1, \phi_2, \cdots, \phi_n \vdash \psi$的一个自然演绎证明。结合可靠性结果有:
当且仅当$\phi_1, \phi_2, \cdots, \phi_n \models \psi$成立,$\phi_1, \phi_2, \cdots, \phi_n \vdash \psi$是有效的。
完备性的用处
与可靠性一样,完备性也是逻辑系统的性质。那么完备性有什么用呢?在一个逻辑系统中,如果我们知道一些前提是真的,即$\phi_1, \phi_2, \cdots, \phi_n$都为真。那么,我们想知道在这样的条件下,结论$\psi$也一定是真吗?即我们想知道$\phi_1, \phi_2, \cdots, \phi_n \models \psi$是否是有效的。那么我们可能想找一个由$\phi_1, \phi_2, \cdots, \phi_n$到$\psi$的证明,即利用推导规则将$\phi_1, \phi_2, \cdots, \phi_n$转化为 $\psi$。这时候,完备性就会告诉我们,如果$\phi_1, \phi_2, \cdots, \phi_n \models \psi$是有效的,那么,这样的证明一定存在。假如你的逻辑系统不满足完备性,那么即使$\phi_1, \phi_2, \cdots, \phi_n \models \psi$是有效的,但是它的证明也可能不存在,那你的努力可能就是徒劳的。
现在我们知道,命题逻辑是可靠的和完备的。
最后,本章给出了一些不同的范式。也给出了SAT求解机通过树状结构来求解使得整个公式为真的每一个原子公式的真值。