谓词逻辑
谓词逻辑(predicate logic)也称作一阶逻辑(first-order logic)。它弥补了命题逻辑在编码诸如存在……,所有……,在……中和只有……等这种判断语句方面的不足。同样的谓词逻辑也是满足合理性和完备性的。
作为形式语言的谓词逻辑
在谓词逻辑中,语法规则较命题逻辑更加复杂表达能力也更强。在谓词逻辑的公式中涉及两种事物:
- 对象:个体、变量或函数符号
- 公式:表示真值
谓词词汇由三个集合构成:谓词符号集$\mathcal{P}$,函数符号集$\mathcal{F}$和常值符号集$\mathcal{C}$。通常将常值看成零元(nullary)函数。是故丢弃常值符号集$\mathcal{C}$。
项
项的定义可以用BNF表示如下:
其中,$x$取遍一个变量的集合$\textbf{var}$,$c$取遍$\mathcal{F}$中的零元函数符号,$f$取遍$\mathcal{F}$中的元$n > 0$的符号。
公式
公式的定义可以用BNF表示如下:
$\phi ::= P(t_1, t_2, \cdots, t_n) ~|~ (\neg \phi)~|~ (\phi \wedge \phi) ~|~(\phi \vee \phi) ~|~(\phi \rightarrow \phi) ~|~ (\forall x \phi) ~|~ (\exists x \phi)$
其中,$P\in \mathcal{P}$是$n \geq 1$元的谓词符号,$t_i$是$\mathcal{F}$上的项,$x$是变量。
Example 2.5 Consider translating the sentence
into predicate logic. As before, the design choice is whether we represent ‘father’ as a predicate or as a function symbol.
1.As a predicate. We choose a constant m for ‘me’ or ‘I,’ so m is a term, and we choose further {S, F, B} as the set of predicates with meanings
Then the symbolic encoding of the sentence above is
saying: ‘For all x and all y, if x is a father of m and if y is a son of x, then y is a brother of m.’
2.As a function. We keep m, S and B as above and write f for the function which, given an argument, returns the corresponding father. Note that this works only because fathers are unique and always defined, so f really is a function as opposed to a mere relation.
The symbolic encoding of the sentence above is now
meaning: ‘For all x, if x is a son of the father of m, then x is a brother of m;’ it is less complex because it involves only one quantifier.
自由变量和约束变量
变量自由与约束与否取决于是否受到量词的约束。在该书中作者采用一种较为复杂但是严谨的对谓词逻辑公式的语法分析树上的叶节点进行描述的办法来判断约束或自由。
代换
变量只是占位符,我们必须用更加具体的信息替代它,使其具有某种含义。给定变量$x$、项$t$和公式$\phi$,定义$\phi[t/x]$为用$t$代替$\phi$中变量$x$的每个自由出现而得到的公式。注意在替换的过程中有时需要进行变量的重命名避免自由变量受到约束。
谓词逻辑的证明论
自然演绎规则
谓词逻辑中自然演绎的证明和命题逻辑中的相似,除此之外,还需要增加新规则以处理量词和相等符号。
相等的证明规则:
推广:
全称量词的证明规则:
存在量词的证明规则:
谓词逻辑的证明论
与命题逻辑中的情形一样,语义必须提供一个独立的、但最终是等价的一种逻辑刻画。所谓“独立”指连接词的含义用不同的方式来定义,在证明论中,通过提供运算解释来定义。在语义学里,我们期望有类似真值表之类的工具。所谓“等价”,指可以证明它的合理性和完备性。
模型
因为谓词逻辑的复杂性,不能简单的对“原子”命题赋真值。我们需要知道每一项的具体含义才能对谓词逻辑中的词汇赋值。所以我们需要一个涉及所有函数和谓词符号的模型。
定义:假设$\mathcal{F}$是函数符号的集合,$\mathcal{P}$是谓词符号的集合,每个符号所需要的变量的个数是固定的。符号对$(\mathcal{F}, \mathcal{P})$的一个模型$\mathcal{M}$由下面的数据集合组成。
- 非空集A是具体值的全集;
- 对每个零元函数$f\in\mathcal{F}$,A中的一个具体元素$f^{\mathcal{M}}$;
- 对每个元数为$n>0$的$f\in\mathcal{F}$,从集合A上$n$元集合$\text{A}^n$到A的具体函数$f^{\mathcal{M}}: \text{A}^n\rightarrow A$;
- 对每个$n>0$元谓词$P\in\mathcal{P},$A上$n$元子集$P^{\mathcal{M}}\subseteq \text{A}^n$。
区分$f$与$f^{\mathcal{M}}$,$P$与$P^{\mathcal{M}}$是非常重要的。$f$和$P$仅仅是符号而已,而$f^{\mathcal{M}}$和$P^{\mathcal{M}}$分别表示模型$\mathcal{M}$中的一个具体函数(或元素)和关系。

这个例子展示了模型的作用,相当于为一系列物理事件建立的模型。
模型的记法是非常自由开放的。选择一个非空集合A,其元素就是显示世界中对象的模型以及具体的函数和关系,分别表示为函数符号和谓词符号。对这些内容仅有一点要求是A上的具体函数和关系作为语法的对应部分,必须有相同个数的变量。
我们需要相对一个环境(relative to an environment)解释公式。可以从不同方面来考虑环境。本质上,它们是所有变量的查询表;这个表$l$将每个变量$x$与它在模型中的值$l(x)$联系起来。因此可以说,环境其实就是从变量集$\textbf{var}$到相关模型中值的论域集合A的函数$l:\textbf{var}\rightarrow A$。给定这样一个查询表,可以指派真值到所有公式。
定义 对于具体值的论域A,一个查询表或环境指的是从变量集$\textbf{var}$到A的函数$l:\textbf{var}\rightarrow A$。对这样的$l$,用$l[x\rightarrow a]$表示将$x$映到$a$并且将其他变量$y$映到$l(y)$的查询表。
最后,给出谓词逻辑公式的语义。显然,我们只需要知道什么情况下其值为T就足够了。
定义 给定关于对$(\mathcal{F}, \mathcal{P})$的模型$\mathcal{M}$和环境$l$,对于$(\mathcal{F}, \mathcal{P})$上的每个逻辑公式$\phi$,通过对$\phi$的结构归纳定义一个满足关系$\mathcal{M}\models_l \phi$。若$\mathcal{M}\models_l \phi$成立,则称在模型$\mathcal{M}$中,相对于环境$l$,$\phi$的赋值为T。
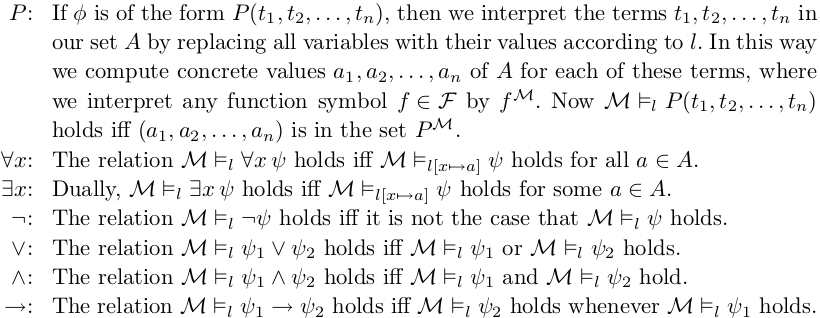
语义推导
语义推导(semantic entailment):给定谓词逻辑的一个公式集$\Gamma$,确定$\Gamma\models \phi$是否有效。

谓词逻辑的不可判定性
在命题逻辑中,给定公式$\phi$,至少原则上我们可以判定$\models \phi$是否成立:总可以使用真值表进行判断。这样的,判断一个谓词逻辑公式是否有效的问题称为判定问题。而在谓词逻辑中,谓词逻辑的公式成立与否是不可判定的。
因其不可判定性,我们还发展了模型检测(model checking)的概念:给定谓词逻辑的一个公式$\phi$和一个相匹配的模型$\mathcal{M}$,确定$\mathcal{M}\models\phi$是否成立。