Relations and Recursion

Partial Orders and Monotonicity

There is three definition in order to undertaken in later chapters required.

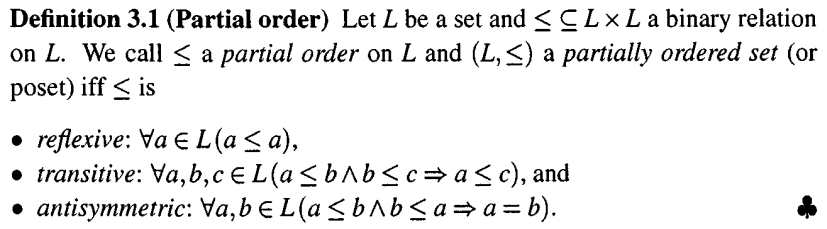
Note that least fixed point is a key concept for characterizing recursion.

Binary Relations

In this section, the important formula is:

We use three operators to express the solution of the formula.

• $r\rightsquigarrow s$ denotes the maxmial solution of the formula in $t$.
• $[t]s$ denotes the maxmial solution of the formula in $r$ the weakest prespecification of t w.r.t. s.
• $\langle t\rangle s$ denotes the dual of the weakest prespecification operator.

Some properties of the three operators are given in this monograph.

Recursion and Termination — the $\mu$-Calculus

This section show the least fixed point is solution of terminated recursion loop. As a example, we looking for a fixed point of the function

The unique solution is $\mathbb{N}\times {0}$.

Relational Semantics of Recursion — the Continuous $\mu$-Calculus

这个有点奇怪,在”面向计算机科学的梳理逻辑”一书中我们发现我们的系统应该属于无限状态空间的情形,并不使用模型检测的方法进行建模。但是这里使用的mu-calculus却是一种模型检测的方法。该方法在System Validation中进行了详细的讲解。这个部分先放弃了,看的云里雾里的,后面需要再回头来研究。